Recursive cell splitting

Source: R/recursiveSplit.R

Uses the celda_C model to cluster cells into population for range of possible K's. The cell population labels of the previous "K-1" model are used as the initial values in the current model with K cell populations. The best split of an existing cell population is found to create the K-th cluster. This procedure is much faster than randomly initializing each model with a different K. If module labels for each feature are given in 'yInit', the celda_CG model will be used to split cell populations based on those modules instead of individual features. Module labels will also be updated during sampling and thus may end up slightly different than yInit.

recursiveSplitCell(
  x,
  useAssay = "counts",
  altExpName = "featureSubset",
  sampleLabel = NULL,
  initialK = 5,
  maxK = 25,
  tempL = NULL,
  yInit = NULL,
  alpha = 1,
  beta = 1,
  delta = 1,
  gamma = 1,
  minCell = 3,
  reorder = TRUE,
  seed = 12345,
  perplexity = TRUE,
  doResampling = FALSE,
  numResample = 5,
  logfile = NULL,
  verbose = TRUE
)

# S4 method for SingleCellExperiment
recursiveSplitCell(
  x,
  useAssay = "counts",
  altExpName = "featureSubset",
  sampleLabel = NULL,
  initialK = 5,
  maxK = 25,
  tempL = NULL,
  yInit = NULL,
  alpha = 1,
  beta = 1,
  delta = 1,
  gamma = 1,
  minCell = 3,
  reorder = TRUE,
  seed = 12345,
  perplexity = TRUE,
  doResampling = FALSE,
  numResample = 5,
  logfile = NULL,
  verbose = TRUE
)

# S4 method for matrix
recursiveSplitCell(
  x,
  useAssay = "counts",
  altExpName = "featureSubset",
  sampleLabel = NULL,
  initialK = 5,
  maxK = 25,
  tempL = NULL,
  yInit = NULL,
  alpha = 1,
  beta = 1,
  delta = 1,
  gamma = 1,
  minCell = 3,
  reorder = TRUE,
  seed = 12345,
  perplexity = TRUE,
  doResampling = FALSE,
  numResample = 5,
  logfile = NULL,
  verbose = TRUE
)

Arguments

x

A numeric matrix of counts or a SingleCellExperiment with the matrix located in the assay slot under useAssay. Rows represent features and columns represent cells.

useAssay

A string specifying the name of the assay slot to use. Default "counts".

altExpName

The name for the altExp slot to use. Default "featureSubset".

sampleLabel

Vector or factor. Denotes the sample label for each cell (column) in the count matrix.

initialK

Integer. Initial number of cell populations to try. Default 5.

maxK

Integer. Maximum number of cell populations to try. Default 25.

tempL

Integer. Number of temporary modules to identify and use in cell splitting. Only used if yInit = NULL. Collapsing features to a relatively smaller number of modules will increase the speed of clustering and tend to produce better cell populations. This number should be larger than the number of true modules expected in the dataset. Default NULL.

yInit

Integer vector. Module labels for features. Cells will be clustered using the celda_CG model based on the modules specified in yInit rather than the counts of individual features. While the features will be initialized to the module labels in yInit, the labels will be allowed to move within each new model with a different K.

alpha

Numeric. Concentration parameter for Theta. Adds a pseudocount to each cell population in each sample. Default 1.

beta

Numeric. Concentration parameter for Phi. Adds a pseudocount to each feature in each cell (if yInit is NULL) or to each module in each cell population (if yInit is set). Default 1.

delta

Numeric. Concentration parameter for Psi. Adds a pseudocount to each feature in each module. Only used if yInit is set. Default 1.

gamma

Numeric. Concentration parameter for Eta. Adds a pseudocount to the number of features in each module. Only used if yInit is set. Default 1.

minCell

Integer. Only attempt to split cell populations with at least this many cells.

reorder

Logical. Whether to reorder cell populations using hierarchical clustering after each model has been created. If FALSE, cell populations numbers will correspond to the split which created the cell populations (i.e. 'K15' was created at split 15, 'K16' was created at split 16, etc.). Default TRUE.

seed

Integer. Passed to with_seed. For reproducibility, a default value of 12345 is used. If NULL, no calls to with_seed are made.

perplexity

Logical. Whether to calculate perplexity for each model. If FALSE, then perplexity can be calculated later with resamplePerplexity. Default TRUE.

doResampling

Boolean. If TRUE, then each cell in the counts matrix will be resampled according to a multinomial distribution to introduce noise before calculating perplexity. Default FALSE.

numResample

Integer. The number of times to resample the counts matrix for evaluating perplexity if doResampling is set to TRUE. Default 5.

logfile

Character. Messages will be redirected to a file named "logfile". If NULL, messages will be printed to stdout. Default NULL.

verbose

Logical. Whether to print log messages. Default TRUE.

Value

A SingleCellExperiment object. Function parameter settings and celda model results are stored in the

metadata

"celda_grid_search" slot. The models in the list will be of class celda_C if yInit = NULL or

celda_CG if zInit is set.

See also

recursiveSplitModule for recursive splitting of feature modules.

Examples

data(sceCeldaCG)
## Create models that range from K = 3 to K = 7 by recursively splitting
## cell populations into two to produce \link{celda_C} cell clustering models
sce <- recursiveSplitCell(sceCeldaCG, initialK = 3, maxK = 7)
#> ==================================================
#> Starting recursive cell population splitting.
#> ==================================================
#> Mon Nov  6 08:01:01 2023 .. Initializing with 3 populations
#> Mon Nov  6 08:01:01 2023 .. Current cell population 4 | logLik: -1225755.01101897
#> Mon Nov  6 08:01:01 2023 .. Current cell population 5 | logLik: -1213677.60126784
#> Mon Nov  6 08:01:01 2023 .. Current cell population 6 | logLik: -1213903.59449854
#> Mon Nov  6 08:01:01 2023 .. Current cell population 7 | logLik: -1214081.54311397
#> Mon Nov  6 08:01:01 2023 .. Calculating perplexity
#> ==================================================
#> Completed recursive cell population splitting. Total time: 0.2422531 secs
#> ==================================================

## Alternatively, first identify features modules using
## \link{recursiveSplitModule}
moduleSplit <- recursiveSplitModule(sceCeldaCG, initialL = 3, maxL = 15)
#> ==================================================
#> Starting recursive module splitting.
#> ==================================================
#> Mon Nov  6 08:01:01 2023 .. Collapsing to 100 temporary cell populations
#> Mon Nov  6 08:01:02 2023 .. Initializing with 3 modules
#> Mon Nov  6 08:01:02 2023 .. Created module 4 | logLik: -1241379.90928455
#> Mon Nov  6 08:01:02 2023 .. Created module 5 | logLik: -1235212.7977535
#> Mon Nov  6 08:01:02 2023 .. Created module 6 | logLik: -1232789.9817561
#> Mon Nov  6 08:01:02 2023 .. Created module 7 | logLik: -1227246.66090571
#> Mon Nov  6 08:01:03 2023 .. Created module 8 | logLik: -1223898.757694
#> Mon Nov  6 08:01:03 2023 .. Created module 9 | logLik: -1221848.26936098
#> Mon Nov  6 08:01:03 2023 .. Created module 10 | logLik: -1220147.96681948
#> Mon Nov  6 08:01:03 2023 .. Created module 11 | logLik: -1220818.37022325
#> Mon Nov  6 08:01:03 2023 .. Created module 12 | logLik: -1221489.07685946
#> Mon Nov  6 08:01:03 2023 .. Created module 13 | logLik: -1222032.53497571
#> Mon Nov  6 08:01:03 2023 .. Created module 14 | logLik: -1222712.17543857
#> Mon Nov  6 08:01:03 2023 .. Created module 15 | logLik: -1223268.97596756
#> Mon Nov  6 08:01:03 2023 .. Calculating perplexity
#> ==================================================
#> Completed recursive module splitting. Total time: 2.128508 secs
#> ==================================================
plotGridSearchPerplexity(moduleSplit)

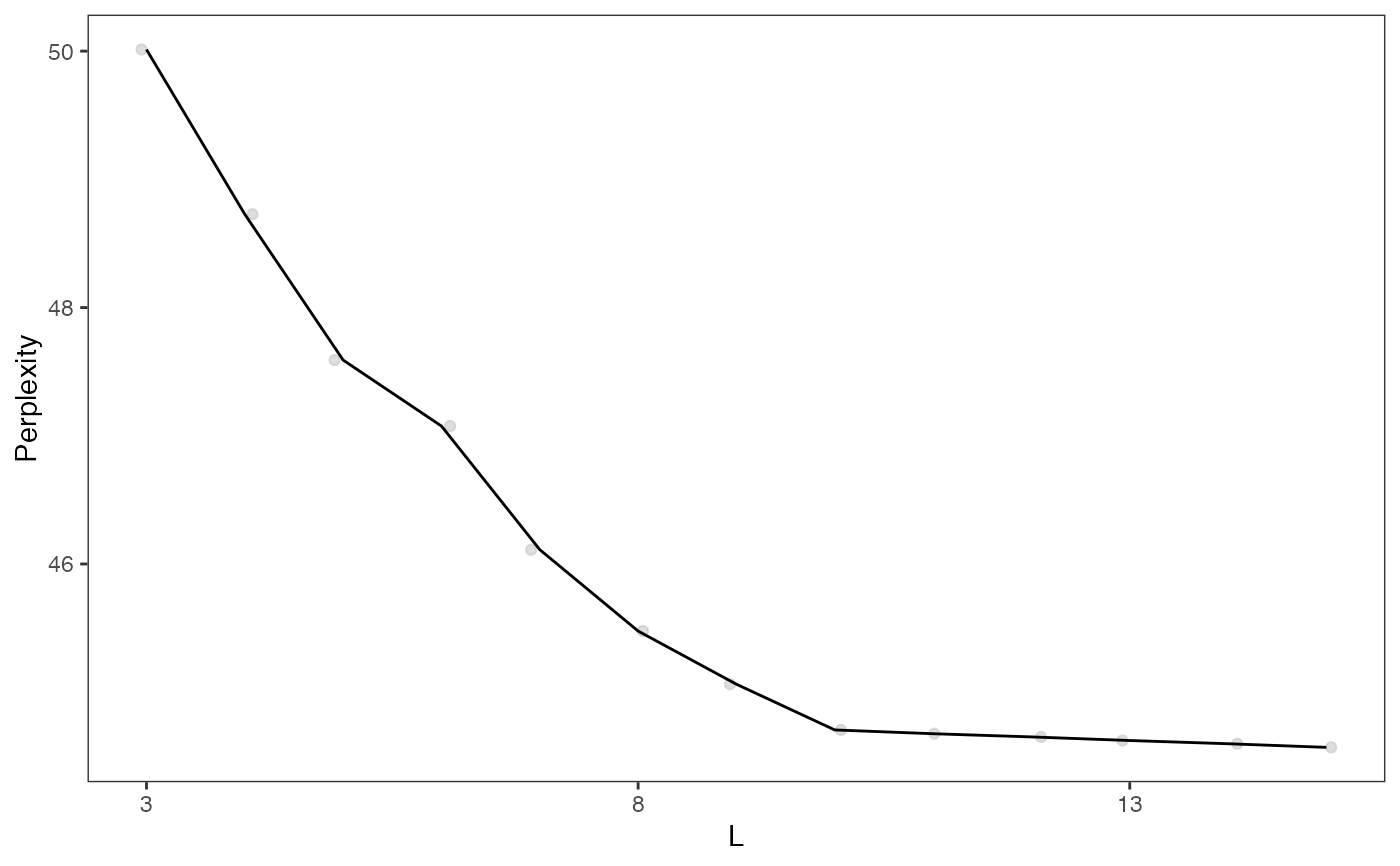moduleSplitSelect <- subsetCeldaList(moduleSplit, list(L = 10))

## Then use module labels for initialization in \link{recursiveSplitCell} to
## produce \link{celda_CG} bi-clustering models
cellSplit <- recursiveSplitCell(sceCeldaCG,
  initialK = 3, maxK = 7, yInit = celdaModules(moduleSplitSelect))
#> ==================================================
#> Starting recursive cell population splitting.
#> ==================================================
#> Mon Nov  6 08:01:04 2023 .. Collapsing to 10 modules
#> Mon Nov  6 08:01:04 2023 .. Initializing with 3 populations
#> Mon Nov  6 08:01:04 2023 .. Current cell population 4 | logLik: -1225286.49558716
#> Mon Nov  6 08:01:04 2023 .. Current cell population 5 | logLik: -1212955.15575681
#> Mon Nov  6 08:01:04 2023 .. Current cell population 6 | logLik: -1212982.74290613
#> Mon Nov  6 08:01:05 2023 .. Current cell population 7 | logLik: -1213005.40337891
#> Mon Nov  6 08:01:05 2023 .. Calculating perplexity
#> ==================================================
#> Completed recursive cell population splitting. Total time: 0.9962049 secs
#> ==================================================
plotGridSearchPerplexity(cellSplit)

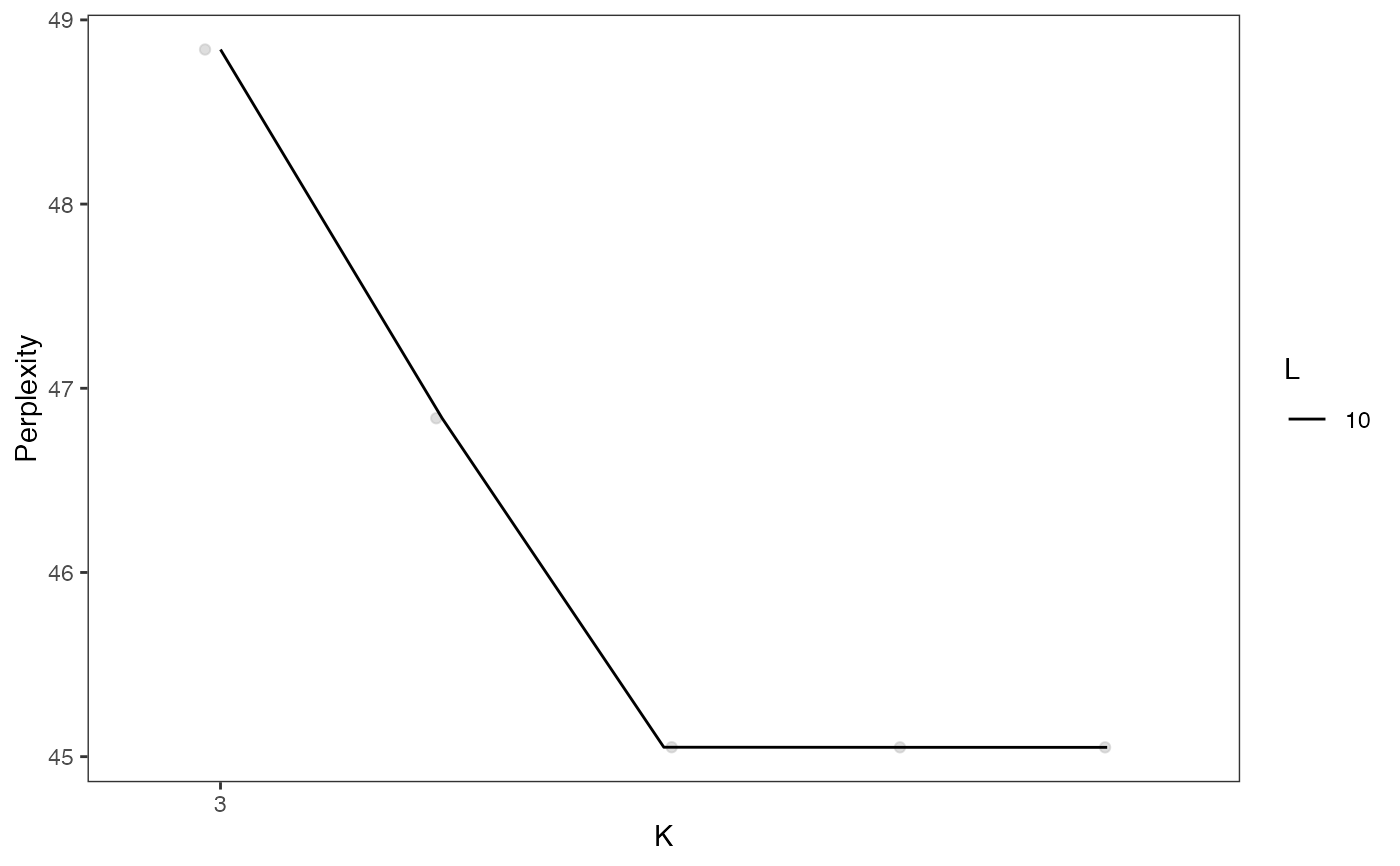sce <- subsetCeldaList(cellSplit, list(K = 5, L = 10))
data(celdaCGSim, celdaCSim)
## Create models that range from K = 3 to K = 7 by recursively splitting
## cell populations into two to produce \link{celda_C} cell clustering models
sce <- recursiveSplitCell(celdaCSim$counts, initialK = 3, maxK = 7)
#> ==================================================
#> Starting recursive cell population splitting.
#> ==================================================
#> Mon Nov  6 08:01:05 2023 .. Initializing with 3 populations
#> Mon Nov  6 08:01:05 2023 .. Current cell population 4 | logLik: -1341630.1679001
#> Mon Nov  6 08:01:05 2023 .. Current cell population 5 | logLik: -1327506.91718317
#> Mon Nov  6 08:01:05 2023 .. Current cell population 6 | logLik: -1315227.54586167
#> Mon Nov  6 08:01:05 2023 .. Current cell population 7 | logLik: -1304393.65802293
#> Mon Nov  6 08:01:05 2023 .. Calculating perplexity
#> ==================================================
#> Completed recursive cell population splitting. Total time: 0.2063239 secs
#> ==================================================

## Alternatively, first identify features modules using
## \link{recursiveSplitModule}
moduleSplit <- recursiveSplitModule(celdaCGSim$counts,
  initialL = 3, maxL = 15)
#> ==================================================
#> Starting recursive module splitting.
#> ==================================================
#> Mon Nov  6 08:01:06 2023 .. Collapsing to 100 temporary cell populations
#> Mon Nov  6 08:01:06 2023 .. Initializing with 3 modules
#> Mon Nov  6 08:01:07 2023 .. Created module 4 | logLik: -1243396.62348886
#> Mon Nov  6 08:01:07 2023 .. Created module 5 | logLik: -1237610.11790137
#> Mon Nov  6 08:01:07 2023 .. Created module 6 | logLik: -1232128.87013396
#> Mon Nov  6 08:01:07 2023 .. Created module 7 | logLik: -1227611.8250329
#> Mon Nov  6 08:01:07 2023 .. Created module 8 | logLik: -1225618.06184004
#> Mon Nov  6 08:01:07 2023 .. Created module 9 | logLik: -1223967.77531912
#> Mon Nov  6 08:01:07 2023 .. Created module 10 | logLik: -1222801.11395987
#> Mon Nov  6 08:01:07 2023 .. Created module 11 | logLik: -1223402.66903597
#> Mon Nov  6 08:01:07 2023 .. Created module 12 | logLik: -1224026.19892208
#> Mon Nov  6 08:01:07 2023 .. Created module 13 | logLik: -1224675.63005464
#> Mon Nov  6 08:01:07 2023 .. Created module 14 | logLik: -1225317.91966369
#> Mon Nov  6 08:01:07 2023 .. Created module 15 | logLik: -1225971.50555157
#> Mon Nov  6 08:01:07 2023 .. Calculating perplexity
#> ==================================================
#> Completed recursive module splitting. Total time: 1.948939 secs
#> ==================================================
plotGridSearchPerplexity(moduleSplit)

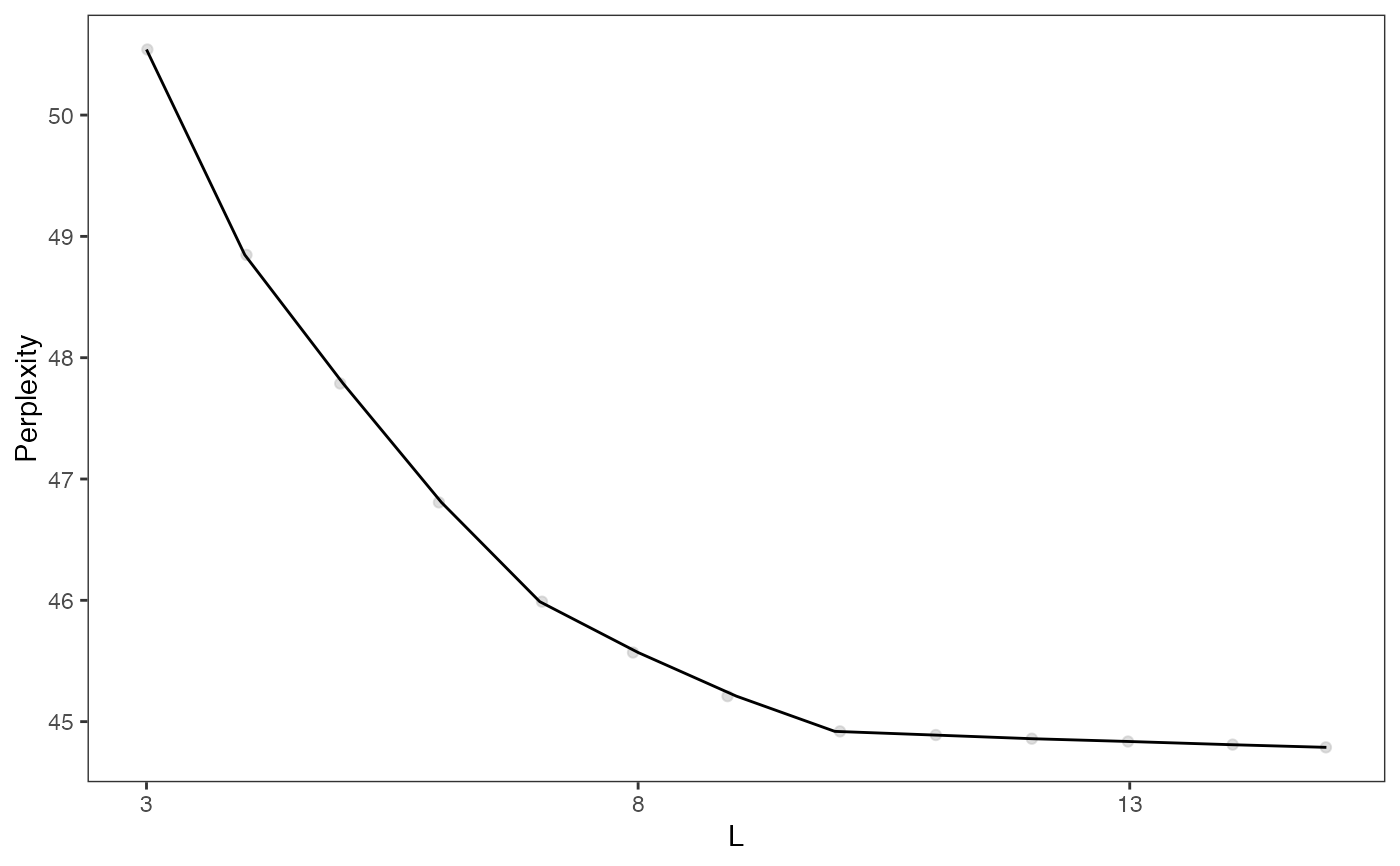moduleSplitSelect <- subsetCeldaList(moduleSplit, list(L = 10))

## Then use module labels for initialization in \link{recursiveSplitCell} to
## produce \link{celda_CG} bi-clustering models
cellSplit <- recursiveSplitCell(celdaCGSim$counts,
  initialK = 3, maxK = 7, yInit = celdaModules(moduleSplitSelect))
#> ==================================================
#> Starting recursive cell population splitting.
#> ==================================================
#> Mon Nov  6 08:01:08 2023 .. Collapsing to 10 modules
#> Mon Nov  6 08:01:08 2023 .. Initializing with 3 populations
#> Mon Nov  6 08:01:10 2023 .. Current cell population 4 | logLik: -1227944.5458832
#> Mon Nov  6 08:01:10 2023 .. Current cell population 5 | logLik: -1215605.08613503
#> Mon Nov  6 08:01:10 2023 .. Current cell population 6 | logLik: -1215627.62281773
#> Mon Nov  6 08:01:10 2023 .. Current cell population 7 | logLik: -1215651.32538066
#> Mon Nov  6 08:01:10 2023 .. Calculating perplexity
#> ==================================================
#> Completed recursive cell population splitting. Total time: 1.931995 secs
#> ==================================================
plotGridSearchPerplexity(cellSplit)

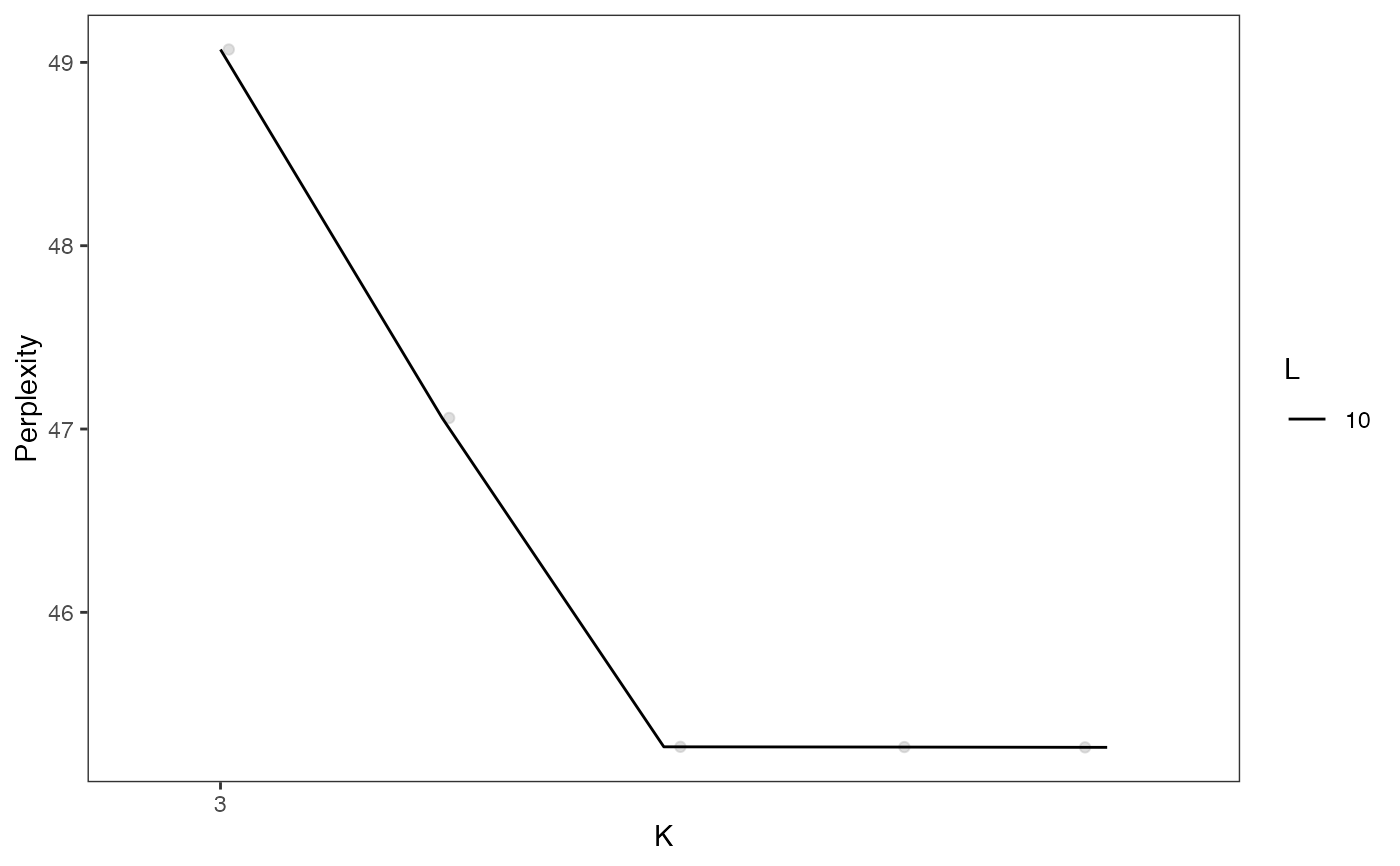sce <- subsetCeldaList(cellSplit, list(K = 5, L = 10))